1. 개요
단층 신경망의 근본적인 한계 때문에 신경망은 필연적으로 다층 구조로 발전할 수 밖에 없었습니다. 하지만 은닉층 하나를 추구하는데 수십 년씩이나 걸렸습니다. 문제는 다층 신경망의 학습 규칙을 찾아내지 못한 데 있었습니다.
앞서 소개한 델타 규칙으로는 다층 신경망을 학습시킬 수 없습니다. 델타 규칙으로 신경망을 학습시키려면 오차가 필요한데, 은닉층의 오차는 아예 정의조차 되어 있지 않기 때문입니다. 출력 노드의 오차는 학습 데이터의 정답과 신경망 출력값의 차이로 정의합니다. 문제는 은닉층 입니다. 은닉층의 노드에는 학습 데이터로부터 주어진 정답이 없습니다. 따라서 은닉층의 오차는 출력 노드와 같은 방식으로는 계산할 수가 없습니다.
1986년에 이러한 문제점은 역전파 backpropagation 알고리즘이 개발되면서 마침내 다층 신경망의 학습 문제가 해결되었습니다. 역전파 알고리즘의 의의는 은닉층 노드들의 오차를 결정한 다음에는, 델타 규칙에 따라 이 오차들로 가중치들을 조절 한다는 게 역전파 알고리즘의 핵심 아이디어입니다.
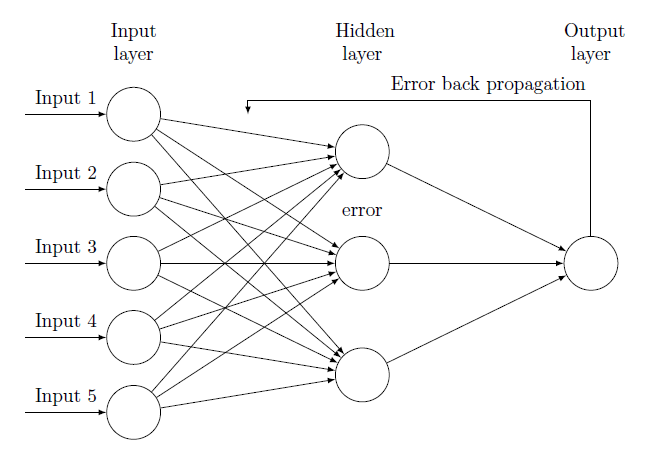
신경망에서 입력 데이터는 입력층에서 은닉층을 거쳐 출력층으로 흘러갑니다. 반면 역전파 알고리즘에서는 위 그림과 같이 신경망의 출력 오차를 출력층에서 시작해 입력층 바로 앞 은닉층까지 역순으로 이동 시킵니다. 이 과정이 마치 출력 오차가 방향으로 퍼져나가는 것과 비슷하다고 해서 역전파 알고리즘이라는 이름이 붙었습니다. 역전파 과정에서도 신호들은 노드 간의 연결선을 따라 흐르고, 해당 연결 가중치를 곱해준다는 점 등은 똑같습니다. 각 노드에서 신호의 입출력 방향이 반대라는 점만 다릅니다.
2. 역전파 알고리즘
은닉 노드들의 문제는 ‘해당 노드의 오차를 어떻게 정의하느냐’입니다. 역전파 알고리즘에서는 바로 아래(다음)에 있는 계층의 델타를 역전파시켜 얻은 가중합으로 오차를 정의합니다. 은닉 노드의 오차는 델타를 역전파시켜 얻은 가중합으로 구하고, 이 값에 활성함수의 도함수 값을 곱해 해당 노드의 델타를 구합니다. 이러한 과정을 출력층에서 시작해 모든 은닉층에 차례대로 반복하는 게 역전파 알고리즘의 핵심입니다.
역전파 알고리즘으로 다층 신경망을 학습시키는 과정을 정리해보겠습니다.
- 신경망의 가중치를 적당한 값으로 초기화한다.
- 학습 데이터 { 입력, 정답 }에서 ‘입력’을 신경망에 입력해 출력값을 얻는다. 이 출력값과 해당 입력의 ‘정답’을 비교해 오차를 구하고, 출력 노드들의 델타를 계산한다.
- 출려 노드의 델타를 역전파시켜 바로 앞(이전) 은닉 노드들의 델타를 계산한다.
- 단계 3을 입력층 바로 앞 은닉층까지 차례로 반복한다.
- 신경망의 가중치를 다음의 학습 규칙으로 변경한다.
- 모든 학습 데이터에 관해 단계 2~5를 반복한다.
- 신경망이 충분히 학습될 때까지 단계 2~6을 반복한다.
출력층의 델타를 역전파시켜 은닉층 노드들의 델타를 구하는 단계 3과 단계4가 추가되기는 했지만, 앞서 소개한 델타 규칙의 학습 절차와 크게 다르지 않습니다.
3. 비용함수와 학습 규칙
비용함수 cost function 는 최적 이론과 관련된 다소 수학적인 개념입니다. 비용함수는 신경망의 지도학습과 관련이 있습니다. 신경망의 지도학습이란 신경망의 가중치를 조절해 학습 데이터에 대한 오차를 줄여가는 과정이라고 설명했습니다. 여기서 신경망의 오차를 측정하는 척도가 바로 비용함수입니다. 신경망의 오차가 크면 비용함수의 값도 크고, 신경망의 오차가 작으면 비용함수도 작은 값을 갖습니다. 신경망의 지도학습에 많이 사용되는 비용함수로는 크게 두 가지 형태가 있습니다.
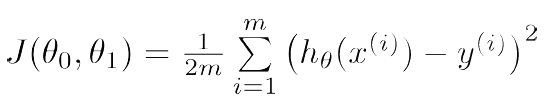
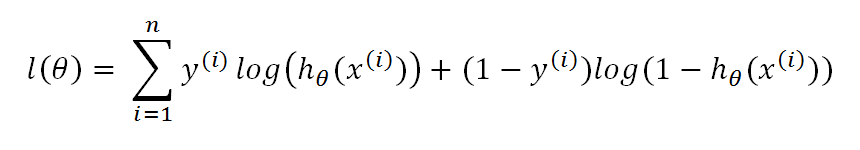
여기서 y는 해당 출력 노드의 출력을, x는 학습 데이터에서 주어진 정답을 의미합니다. n과 m은 각각 출력 노드의 개수를 나타냅니다.
먼저 첫번째 식의 비용함수 Sum of squared error 에 관해 살펴보겠습니다. 이 비용함수는 신경망의 출력과 정답의 오차를 제곱한 형태입니다. 신경망의 출력(y)이 정답(x)와 같으면, 오차는 0이 됩니다. 반대로 두 값의 차이가 커지면 커질수록 오차의 값도 커집니다.
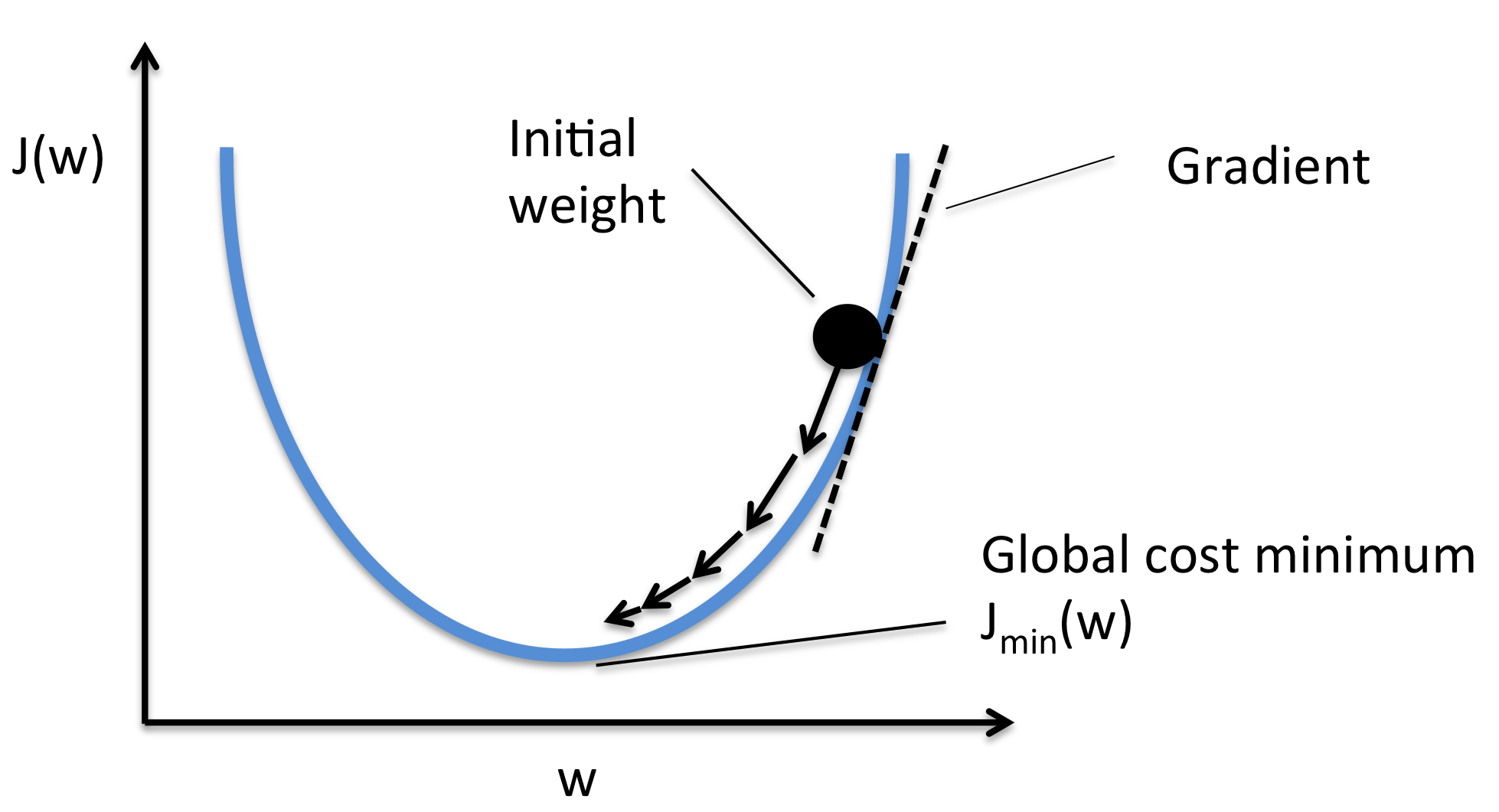
비용함수의 값이 오차에 비례하는 걸 알 수 있습니다. 사실 이 비용함수와 오차의 관계는 따로 설명이 필요 없을 정도로 직관적입니다. 신경망 연구 초기에는 대부분의 이 비용함수로부터 유도한 학습 규칙을 사용했습니다. 다층 신경망의 학습 규칙인 역전파 알고리즘도 처음에는 이 함수로부터 유도되었고, 회귀 문제의 경우에는 여전히 이 비용함수를 사용합니다.
이제 두번째 식의 비용함수 Cross entropy 함수 에 대해 알아보겠습니다. 일단 앞의 수식을 보면 로그(ln) 함수 때문에 신경망의 출력(y)은 0~1 사이의 값이어야 합니다. 이런 이유로 Cross Entropy 비용 함수는 활성함수로 시그모이드 함수나 소프트맥스 함수를 채택한 신경망과 함께 사용되는 경우가 많습니다.
다음 그래프는 x=1일 때 비용함수의 그래프입니다.
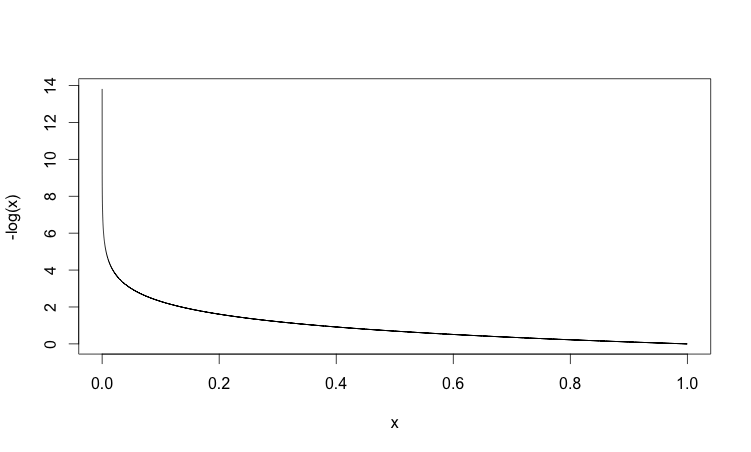
신경망의 출력, y가 1일 때, 즉 오차(d-x)가 0일 때는 비용함수의 값도 0입니다. 반면, 신경망의 출력 y가 0에 가까울수록, 즉 오차가 커질수록 비용함수의 값이 급격하게 커집니다. 이 때 이 비용함수는 오차의 크기에 비례합니다.
다음 그래프는 x=0일 때 비용함수의 그래프입니다.
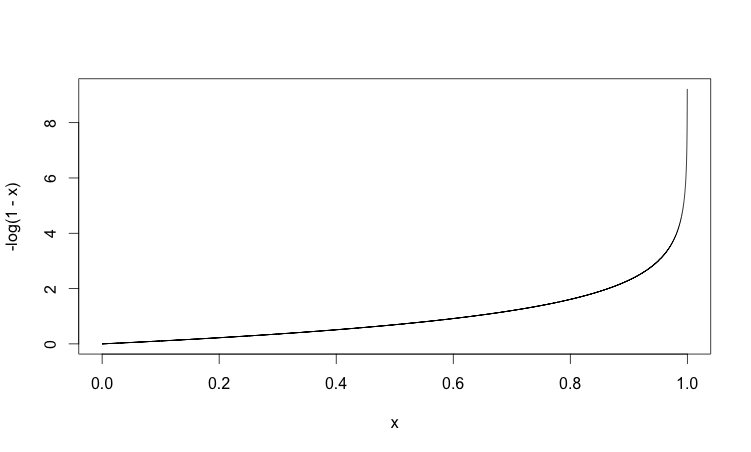
신경망의 출력(y)이 0일 때, 즉 오차가 0일 때는 함수의 값이 0입니다. 신경망의 출력이 1에 가까워지면, 즉 오차가 커지면 함수의 값도 급격하게 커집니다. 역시나 비용함수는 오차의 크기에 비례합니다.
Cross Entropy 함수로 표현된 비용함수가 첫번째 식에 보인 제곱합 형태의 비용함수와 가장 크게 다른 점은 오차에 기하급수적으로 비례하는 함수 라는 사실입니다. 즉 같은 오차라도 Cross Entropy 함수가 훨씬 더 민감하게 반응합니다.
어떤 비용함수를 채택하느냐에 따라 학습 규칙, 즉 역전파 알고리즘의 수식이 달라지기 때문입니다. 구체적으로 출력 노드의 델타를 계산하는 수식이 약간 달라집니다. 다음은 출력 노드의 델타를 계산하는 수식이 약간 달라집니다. 다음은 출력 노드의 활성함수가 시그모이드 함수일 경우에 Cross Entropy 함수로부터 유도된 역전파 알고리즘으로 다층 신경망을 학습시키는 과정입니다.
- 신경망의 가중치를 적당한 값으로 초기화합니다.
- 학습 데이터 { 입력, 정답 }에서 ‘입력’을 신경망에 입력해 출력값을 얻습니다. 이 출력값과 해당 입력의 ‘정답’을 비교해 오차를 구하고, 출력 노드들의 델타를 계산합니다.
- 출력 노드의 델타를 역전파시켜 바로 앞 은닉 노드들의 델타를 계산합니다.
- 단계 3을 입력층 바로 앞 은닉층까지 차례로 반복합니다.
- 신경망의 가중치를 다음의 학습 규칙으로 변경합니다.
- 모든 학습 데이터에 관해 단계 2~5를 반복합니다.
- 신경망이 충분히 학습될 때까지 단계 2~6을 반복합니다.
딥러닝은 대부분 Cross entropy 함수로부터 유도된 학습 규칙으로 신경망을 학습시킵니다. 학습 속도와 성능이 훨씬 낫기 때문입니다.
