데이터의 분포 특성을 알기 위해서 적절한 확률밀도함수를 가정하여 데이터 분포에 대한 모델을 만드는 것을 확률 모델 이라 한다. 가장 대표적으로 사용되는 모델로 가우시안 확률 모델이 있다. 이는 하나의 클래스 혹은 관찰된 전체 데이터 집합이 평균을 중심으로 하여 하나로 뭉쳐져 있는 분포 형태를 표현하는데 적합한 확률 모델이다.
주어진 데이터에 대하여 가우시안 확률분포를 이용하여 모델을 설정하는 것은 가장 널리 사용되는 방법이다. 그러나 가우시안 확률분포는 기본적으로 데이터들이 평균을 중심으로 하나의 그룹으로 뭉쳐 있는 유니모달(unimodal) 형태를 가진다는 것을 가정하고 있어서, 복잡한 분포 형태를 가지는 데이터의 확률밀도함수를 표현하기는 힘들다는 문제점이 있다. 따라서 복잡한 데이터 분포를 추정하기 위해서는 보다 일반적인 형태를 표현할 수 있는 확률 모델이 필요하며, 이때 가장 손쉽게 생각해 볼 수 있는 것이 여러 개의 가우시안을 합하여 만들어지는 모델이다. 이를 가우시안 혼합 모델(Gaussian Mixture Model) 이라고 한다.
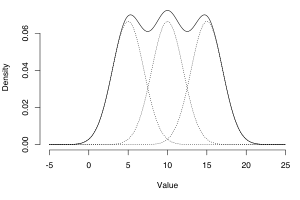
이와 같이 복수 개의 가우시안 분포들의 합으로 새로운 확률분포를 나타내는 가우시안 혼합 모델을 사용하면, 하나의 가우시안 분포함수로 나타낼 수 없었던 분포 특성을 잘 나타낼 수 있을 뿐만 아니라, 아무리 복잡한 형태의 함수라도 충분한 개수의 가우시안 함수를 사용하기만 하면 원하는 만큼 정확하게 근사해 낼 수 있다. 가우시안 혼합 모델을 이용하여 밀도함수가 추정되면, 이를 이용하여 베이즈 분류기를 설계할 수도 있으며, 또한 K-means 클러스터링과 같은 군집화에도 적용할 수 있을 것이다.
