1. 개요
머신러닝 문제로는 크게 ‘분류’와 ‘회귀’ 문제가 있습니다. 분류는 입력 데이터가 어느 범주에 속하는지를 알아내는 문제입니다. 스팸 메일 분류기나 문자 인식기 등이 대표적인 분류 문제입니다. 반면 회귀 문제는 범주가 아니라 값을 추정한다는 점이 다릅니다. 예를 들어 교육 수준과 나이를 알 때, 연봉이 어느 정도나 될지를 예측하는 게 회귀 문제입니다.
신경망은 분류 문제와 회귀 문제에 모두 사용할 수 있지만, 회귀 문제에 쓰는 경우는 많지 않습니다. 대부분의 회귀 문제는 신경망처럼 복잡한 모델을 사용하지 않고도 해결되기 때문입니다.
분류할 범주가 2개인지 그 이상인지에 따라 출력 노드의 개수와 활성함수가 달라집니다. 은닉 노드와는 관계가 없고, 출력층의 노드만 영향을 받는다는 사실에 주의하기 바랍니다.
2. 이진 분류 Binary classification
입력 데이터를 둘 중의 하나로 분류하는 이진 분류기는 의외로 쓸모가 많습니다. 스팸 메일의 판별(스팸 또는 정상)이나, 대출 승인(승인 또는 거절) 등이 대표적인 이진 분류 문제입니다.
범주가 2개인 경우에는 신경망의 출력 노드가 1개만 있으면 됩니다. 출력 노드의 출력이 기준값 이상인지 아닌지로 입력 데이터의 범주를 판별할 수 있기 때문입니다. 예를 들어 출력 노드의 활성함수로 시그모이드 함수를 사용한다면 신경망의 출력이 0.5 이상인지 여부로 범주를 판별하면 됩니다. 시그모이드 함수의 출력 범위가 0~1 사이이므로, 중간값인 0.5를 기준으로 범주를 결정하는 겁니다.
다음과 같은 이진 분류 문제를 예로 들어 보겠습니다.
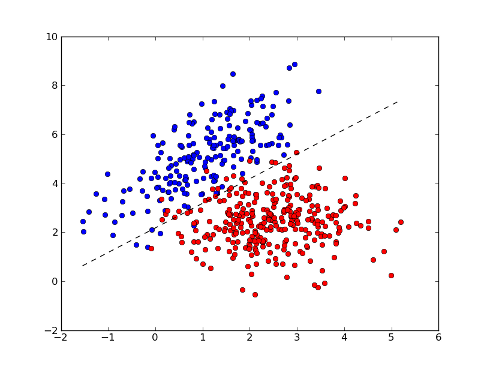
이 경우에 학습 데이터는 다음과 같은 형태로 주어집니다. 처음 2개의 숫자는 각각 x좌표, y좌표이고, 세 번째 기호는 해당 데이터가 속하는 범주를 나타냅니다. 지도학습용 데이터이므로 입력과 정답이 같이 주어집니다. 신경망은 0~1 사이의 숫자를 출력하는데, 정답은 빨간점, 파란점과 같은 기호로 주어졌습니다. 이러면 오차를 계산할 수 없으므로 학습 데이터의 범주 이름을 범주1은 1로, 범주2는 0으로 바꿔줘야 합니다.
| { 5, 7, 범주1 } |
| { 9, 8, 범주2 } |
| … |
| { 6, 5, 범주2 } |
이진 분류 신경망의 학습에는 Cross entropy 함수를 비용함수로 사용하는 게 일반적입니다. 은닉 노드와 출력 노드의 활성함수로는 시그모이드 함수를 사용합니다.
- 이진 분류 신경망에서 출력층은 1개의 노드로 구성한다. 활성함수로는 시그모이드 함수를 사용한다.
- 학습 데이터의 범주 이름은 각각 시그모이드 함수의 최대값과 최소값을 할당해 숫자로 바꿔준다.
- 신경망의 가중치를 적당한 값으로 초기화한다.
- 학습 데이터 { 입력, 정답 }에서 ‘입력’을 신경망에 입력해 출력값을 얻는다. 이 출력값과 해당 입력의 ‘정답’을 비교해 오차를 구하고, 출력 노드들의 델타를 계산한다.
- 출력 노드의 델타를 역전파시켜 바로 앞 은닉노드의 델타를 계산한다.
- 단계 5의 입력층 바로 앞 은닉층까지 차례로 반복한다.
- 신경망의 가중치를 해당 학습 규칙으로 변경한다.
- 모든 학습 데이터에 관해 단계 4~7을 반복한다.
- 신경망이 충분히 학습될 때까지 단계 4~8을 반복한다.
3. 다범주 분류 Multiclass classification
범주가 3개 이상인 분류 문제를 신경망으로 해결하는 방법을 알아보겠습니다. 다음과 같이 평면상의 좌표(x, y)가 입력으로 주어졌을 때, 3개의 범주 중에서 해당 범주를 판별하는 문제를 예로 들어 보겠습니다.
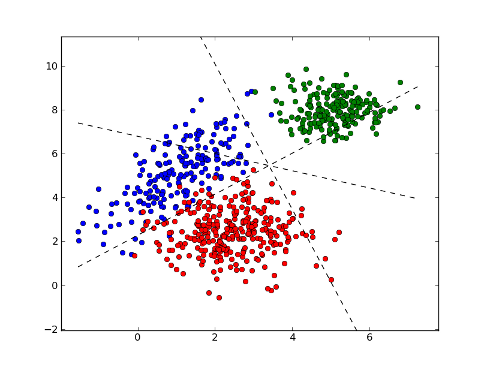
먼저 신경망을 구성해야 합니다. 입력이 2개이므로 입력층 노드는 2개를 사용합니다. 출력 노드의 개수도 정해야 하는데, 범주가 3개 이상인 분류 문제에서 출력 노드는 범주와 같은 개수를 사용하는 게 가장 좋습니다. 따라서 범주가 3개이므로 출력 노드도 3개를 사용합니다.
학습 데이터는 다음과 같은 형태로 주어집니다. 각 데이터에서 처음 2개의 숫자는 각각 x좌표, y좌표이고, 세 번째 값이 해당 좌표가 속하는 범주를 나타냅니다. 지도학습용 데이터이므로 입력과 정답이 같이 주어집니다.
| { 5, 7, 범주1 } |
| { 9, 8, 범주3 } |
| { 2, 4, 범주2 } |
| … |
| { 6, 5, 범주3 } |
오차를 계산하려면 학습 데이터의 범주 이름을 숫자 형태로 바꿔줘야 합니다. 이번에는 신경망의 출력 노드가 3개인 점을 고려하여 다음과 같은 벡터 형태로 바꾸도록 하겠습니다.
| 범주1 -> [ 1 0 0 ] |
| 범주2 -> [ 0 1 0 ] |
| 범주3 -> [ 0 0 1 ] |
위 변환은 각 출력 노드마다 범주를 하나씩 대응시켜 놓고, 해당 범주의 출력 노드만 ‘1’을 출력하도록 하겠다는 의미입니다. 예를 들어 입력 데이터가 범주 2에 속한다면, 두 번째 출력 노드만 1을 출력하고 나머지 출력 노드는 0을 출력해야 정답입니다. 이러한 표현 기법을 ‘one-hot 인코딩’ 또는 ‘1-of-N 인코딩’이라고 합니다. 출력 노드의 수를 범주의 개수와 똑같이 만든 이유도 이러한 인코딩 기법을 적용하기 위해서입니다. 이제 신경망의 최종 학습 데이터는 다음과 같은 형태가 됩니다.
| { 5, 7, [ 1 0 0 ] } |
| { 9, 8, [ 0 0 1 ] } |
| { 2, 4, [ 0 1 0 ] } |
| … |
| { 6, 5, [ 0 0 1 ] } |
이제 출력 노드의 활성함수를 정해야 합니다. 다범주 분류기는 출력 노드의 활성함수로 소프트맥스 softmax 함수를 사용하는 게 일반적입니다.
시그모이드 함수 등 지금까지 살펴본 활성함수는 자신의 노드로 들어오는 신호의 가중합만을 고려해 출력값을 계산했습니다. 즉 다른 출력 노드의 계산에는 일절 관여하지 않았습니다. 하지만 소프트맥스 함수는 자신의 가중합뿐만 아니라, 다른 출력 노드들의 가중합도 고려합니다.
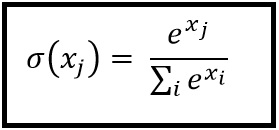
만약 출력 노드의 활성함수로 시그모이드 함수를 사용할 경우, [ 1 1 1 ] 과 같은 데이터가 주어졌을 때 범주1에 속할 확률이 100%, 범주2에 속할 확률이 100%, 범주3도 100%입니다. 따라서 이 경우에 각 범주에 해당될 실제 확률은 1/3입니다. 이처럼 다범주 분류 신경망에서 출력값을 제대로 해석하려면 다른 출력 노드와 상대적인 크기를 비교 해봐야 합니다.
소프트맥스 함수는 각 출력 노드의 출력을 0~1로 제한할 뿐만 아니라, 출력 노드의 출력을 모두 합한 값이 항상 1이 되게 만들어줍니다. 이처럼 소프트맥스 함수는 모든 출력값의 상대적인 크기를 고려한 값을 출력하기 때문에, 다범주 분류 신경망에 적합합니다.
이제 다범주 분류 신경망의 학습 규칙에 관해 알아보겠습니다. 이진 분류 신경망과 마찬가지로 다범주 분류 신경망도 Cross entropy 함수로 유도한 학습 규칙을 사용하는 게 일반적입니다. 학습 성능이 뛰어날 뿐만 아니라 학습 규칙도 간단해지는 장점이 있기 때문입니다.
다범주 분류 신경망의 학습 절차를 정리해보겠습니다.
- 다범주 분류 신경망에서 출력층은 분류할 범주와 같은 개수의 출력 노드로 구성한다. 활성함수로는 소프트맥스 함수를 사용한다.
- 학습 데이터의 범주 이름은 one-hot 인코딩을 통해 벡터 형태로 바꿔준다.
- 신경망의 가중치를 적당한 값으로 초기화한다.
- 학습 데이터 { 입력, 정답 }에서 ‘입력’을 신경망에 입력해 출력값을 얻는다. 이 출력값과 해당 입력의 ‘정답’을 비교해 오차를 구하고, 출력 노드들의 델타를 계산한다.
- 출력 노드의 델타를 역전파시켜 바로 앞 은닉 노드들의 델타를 계산한다.
- 단계 5를 입력층 바로 앞 은닉층까지 차례로 반복한다.
- 신경망의 가중치를 다음의 학습 규칙으로 변경한다.
- 모든 학습 데이터에 관해 단계 4~7을 반복한다.
- 신경망이 충분히 학습될 때까지 단계 4~8을 반복한다.
